Philosophical maintenance

"Laws of nature are human inventions, like ghosts. Laws of logic, of mathematics are also human inventions, like ghosts. The whole blessed thing is a human invention, including the idea that it isn’t a human invention. The world has no existence whatsoever outside the human imagination. It’s all a ghost, and in antiquity was so recognized as a ghost, the whole blessed world we live in. It’s run by ghosts. We see what we see because these ghosts show it to us, ghosts of Moses and Christ and the Buddha, and Plato, and Descartes, and Rousseau and Jefferson and Lincoln, on and on and on. Isaac Newton is a very good ghost. One of the best. Your common sense is nothing more than the voices of thousands and thousands of these ghosts from the past. Ghosts and more ghosts. Ghosts trying to find their place among the living."

Want to read more? 'Zen and the Art of Motorcycle Maintenance' can be read in its entirety here.

What is a proof?

Formally, a mathematical proof is a sequence of expressions in a formal language. An expression can be entered in the sequence if it follows from earlier expressions using rules of inference also expressed in the formal language, or if it belongs to a finite set of expressions called axioms. The last expression in the sequence is what the proof proves. It is called a theorem.

In real life, mathematicians do not prove their theorems in formal languages. Basically this is the accepted definition of a mathematical proof: 'A proof is a proof until proved otherwise'

To prove things can make you rich. This page lists puzzles worth between 50 and more than a million dollars. Click here to read how 'The Eternity Puzzle' made someone 1.6 million richer. One million is waiting for the first to settle Riemann's hypothesis.

A proof of Riemann hypothesis 'is perhaps the most tantalising goal in mathematics today. If true, it tells us that prime numbers, which are those exactly divisible only by one and themselves, are scattered utterly randomly along the number line. If not, then mathematicians may be able to predict where the prime numbers fall.' - Source

Some time ago Louis de Branges de Bourcia, a professor of mathematics at Purdue University in Indiana, issued a press release claiming he had proved the Riemann hypothesis is true. He can not collect the prize money straight away: 'To claim the one million dollar prize money put up by the Clay Mathematics Institute in Cambridge, Massachusetts, de Branges must first publish his paper in a journal and then the work must survive two years of scrutiny by the mathematics community.'

A lot of mathematics deals with infinity in one form or another. Click here to take it for a spin.

Mathematics is not mathematics

We mathematicians are used to the fact that our subject is widely misunderstood, perhaps more than any other subject (except perhaps linguistics). Misunderstandings come on several levels.

One misunderstanding is that the subject has little relevance to ordinay life. Many people are simply unaware that many of the trappings of the present-day world depend on mathematics in a fundamental way. When we travel by car, train, or airplane, we enter a world that depends on mathematics. When we pick up a telephone, watch television, or go to a movie; when we listen to music on a CD, log on to the Internet, or cook our meal in a microwave oven, we are using the products of mathematics. When we go into hospital, take out insurance, or check the weather forecast, we are reliant on mathematics. Without advanced mathematics, none of these technologies and conveniences would exist.

Another misunderstanding is that, to most people, mathematics is just numbers and arithmetic. In fact, numbers and arithmetic are only a very small part of the subject. To those of us in the business, the phrase that best describes the subject is "the science of patterns," a definition that only describes the subject properly when accompanied by a discussion of what is meant by "pattern" in this context.

Read the entire article by mathematician Keith Devlin here.

To add or multiply, that is the question.

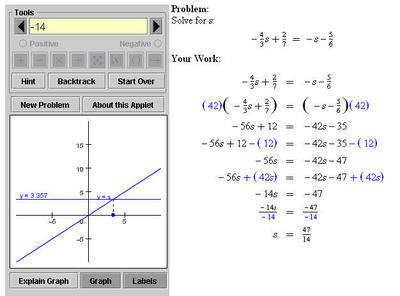
- I am trying to calculate 2 + 3 * 5.
- OK.
- Tell me, should I add or multiply first?
- Does it matter?
- Sure it matters!
- How do you know?
- OK. Let me check it out.
- I like this.
- What is it that you like?
- That you are going to check it out.
- If I add first and then multiply I get 25. But if I multiply first and then add I get 17.
- So which one is right?
- They can't both be right?
- Don't be silly!
- OK
- My calculator gives me the answer 25, but my friend's calculator gives 17.
- You know what?
- No.
- In Poland they would write 23+5* or 235*+.
- How much is 23+5*?
- They start from the left. First comes a 2, so they remember that number. Then comes a 3 so they remember that number too.
- They have to remember a lot?
- (Smiles) Yes, but then comes a +, so they add the two numbers they have remembered to get 5. Then comes another 5.
- So now they remember two 5s?
- Which gives 25 when they see the * sign.
- Neat! But what about 235*+?
- Why don't you tell me?
- OK. I'll have a go. They first remember the numbers 2, 3 and 5.
- OK
- Then the * tells them to multiply, but which numbers?
- What do you think?
- The two last ones?
- Right.
- So they get 15.
- And what happens when they see the +?
- They add the two numbers on their mind.
- Which are?
- 2 and 15.
- You are smart! You know that?
- Can I try another one? One that does not give neither 17 nor 25.
- No problem. Try this one: 235+*.
- (Thinking for a while) The + gives me 8, and the * means 2 * 8, so the answer is 16.
- Give me one more.
- Why don't you make up one?
- OK! Let me try 23*5+.
- Go ahead.
- (Very fast) 11.
- Excellent!
- I like this way to calculate!
- Why is that?
- Because I never wonder if I should add or multiply first. As soon as I see a + sign I add the two last numbers, and if I see a * I multiply.
- (Smiling) I am happy for you!
- And one more thing. When I calculate I start from the left reading one thing at a time without worrying about what comes next. What follows does not matter. You know what my father always says?
- No, tell me.
- It his favourite saying. "Let's cross the bridge when we come to it."
- Many calculators and computers convert the expressions to this form before they calculate for that reason. The form is called RPN, or Reverse Polish Notation.
- Did Einstein come up with this system?
- No, his name was Jan Lukasiewicz.
- In the 1920s.
- Tell me. If this system is so wonderful, why is it not used all over the place?
- I don't know. Tradition maybe.
I like talking with you. This Polish things and stuff. It makes me think.
- I am glad you feel like that.
- But you know what? We haven't solved my problem. In 2 + 3 * 5, should I add or multiply first?
- Ah, yes, that one. Where did you get the problem from?
- From the textbook.
- Did it say "Sue ate 2 pancakes in the morning and 3 in the afternoon for 5 days. How many pancakes did she eat in all?"
- Then I would add 2 and 3 before multiplying with 5, but it didn't say that.
- Did it say "Sue ate 2 pancakes on Monday and then 3 pancakes every day for 5 days."
- I get your point! That would mean that I should first multiply 3 and 5 and afterwards add 2. But it said neither. It just said "2 + 3 * 5 = ?"
- The convention is to start with the operations from the left.
- So I should add before I times?
- Well, only if the operations have the same priority.
- Do + and * have the same priority?
- Multiplication has a higher priority.
- So I should times first?
- Yes.
- So the answer is 17.
- Correct.
- So it would be wrong to add first?
- Yes. If you want to add first you would have to add some parenthesis. (2 + 3) * 5.
- So anything inside paranthesis should be calculated first?
- Yep.
- You know what? In Poland they have a much simpler system!

Solving equations a step at a time

Here you get help to solve equations one step at a time:

1. Type a number or expression in the yellow textbox.
2. Use the calculator buttons to add, subtract, multiply, or divide from each side of the equation. Hover your mouse over each button to see what it does.
3. Watch the results of your work on the right.
4. Continue until you've solved the equation.
5. Just click on the New Problem button to practice again.

To get it to work you have to install a plug-in and it will only work in Internet Explorer.

About the people behind the site:

StudyWorks! Online is a free learning site delivering innovative learning tools to help students develop an understanding of math and science concepts. StudyWorks Online gives students, parents, and teachers access to high quality content, interactive activities, real world examples, and monitored homework help through the Homework Help Collaboratory.

Sally

More Peanut strips.

Get hooked on codes

The Code Book, The Secret History of Codes and Code Breaking was written by Simon Singh. You can now download it for free here.

'The aim of the project was to create an interactive version of The Code Book, so that readers could encrypt, break codes and see how the Enigma machine really works. However, it soon became clear that the CD-ROM had a huge potential for getting young people interested in mathematics.'

Wanted: Math Teachers!

This was in the news a few days ago:

IBM to Encourage Employees to Be Teachers

International Business Machines Corp., worried the United States is losing its competitive edge, will financially back employees who want to leave the company to become math and science teachers.

More

By the way, if you want to keep track of what's happening in the world of math education try a Google Alert:

Google Alerts are email updates of the latest relevant Google results (web, news, etc.) based on your choice of query or topic.

Back to basics

Distance and angle are two basic terms in mathematics. What would happen if they were replaced by other terms? It is a refreshing question asked by N J Wildberger this fall.

For separation of points, quadrance is defined as the distance squared. Easy enough. It eliminates a few square-root signs. Pythagoras' is simply a + b = c when a, b , and c are the quadrances of the sides in a right-angled triangle.

For separation of lines, spread is defined as the square of the sine of the acute angle between the lines.

From these definitions he demonstrates the triple quad formula, the spread law, the cross law, and the triple spread formula. With these you are armed to solve most basic trigonometry questions.

Download the first chapter of his soon to be published book here. This is his home page.

Wildberger's fresh ideas is an excellent playground where you can set your students free to develop some math on their own.

Kitchen Table Math is about doing math with children is the web place where I found this exciting news. Hereby recommended.

Patterns in election data

There were 13,118 registered voters at the election held in May this year. 10,005 of them voted, or 76%.

Give students the raw data and they may discover several patterns.

This is what I found:

1. A candidate who got more than 32.7% of the registered voters' vote was elected to the Legislative Assembly regardless of district.

2. A candidate who got more than 42% of the votes cast was elected to the Legislative Assembly regardless of district.

The big winner, in my mind, was Anthony Eden. 75% of those who voted in Bodden Town voted for him.

Here is my spreadsheet file. Strip it for columns E and F before you give it to students.

What does a mathematician look like?

To me, a mathematician is someone who creates mathematics, not one who teaches it. But, what does a mathematician look like?

Which of the two gentlemen above is a mathematician? Hint: the other one is a teacher of buddhism. Click here and here to see if you guessed correctly, and here to see more pictures of today's mathematicians.

Mafalda is wondering

Quino is the artist beyond Mafalda.

First name statistics

When I was born in 1952 in Norway, Jan was the most popular name to give a baby. The graph above shows that the name Jan is losing popularity, while Mathias (see below) is the most popular name today.



Source.

What is the most popular name in Cayman from year to year? I don't know, and I can not find any website for the government's statistical office.

At John Gray High School two years ago Michael and Priscilla were the most popular names for boys and girls respectively. Why not take a statistics at your school and email it to CayMath?

Musical math comedy

"The Calculating Mr. One is a musical comedy that explores importance of mathematics and problem solving in everyday life and is based on the National Curriculum for Maths and the Numeracy Targets. It's also interactive with the audience required to solve mathematical problems in order for play to progress."

If you like to get emails with news like the above, send an email to enews@atm-online.org.uk with the word 'subscribe' in the subject box. ATM stands for Association of Teachers of Mathematics.

Black box

Black Box is a logical game.

A black box contains several balls that reflect laser beams. Your task is to fire beams, and based on where the beams come out of the box, deduce where the balls are.

Inversions

An inversion is a word or name written so it reads in more than one way. Try to read the text above standing on your head. More text inversions.



If you want to keep your youth, don't turn up-side-down! More image inversions.

Why not try to create an inversion?! Email it to CayMath and we will publish it here.

A page for each day of the month

11 is a prime number.

1, 3, 4, 7, 11, 18, 29...
A Lucas number.

The Eleven Plus was an English school selection examination taken by 11 year olds which was abolished in most areas with the introduction of comprehensive schools. It is still fondly remembered by taxi drivers and education ministers.

Richard Phillips has written a page for each day of the month. Read more about 11 here.

Elementary logic

Cartoon by Sidney Harris.

By the way, who were Leibniz, Boole, and Gödel?

Another 5 numbers

"Following on from the original series, exploring numbers from zero to infinity, Simon Singh uncovers the mathematical, social and scientific history and significance of another five numbers, over five exploratory episodes.

These numbers have been at the centre of some of mathematics' most challenging problems and Simon reveals their historical, practical and esoteric merits. Along the way we get to grips with the search for the largest prime number, which serves as a tool for the encoding and encryption of information on the internet. Whilst in the casinos of America, mathematicians are making gambling heads roll: why is the number 7 so influential in properly shuffling a pack of cards?"

Listen.

How much is 8 x 6?

"If you can't solve the given problem, solve first a simpler problem."

- How much is 8 x 6?
- I don't know, but I know that 2 x 6 = 12.
- So?
- Eight sixes is two sixes less than ten sixes, so 8 x 6 = 60 - 12 = 48.

- How much is 8 x 6?
- I don't know, but I know that 8 x 5 = 40.
- So?
- Six eights is 8 more than five eights, so 8 x 6 = 40 + 8 = 48.
- Six eights? The question was eight sixes!
- Same thing!
- Ah, yes!

- How much is 8 x 6?
- More than 5 x 5 = 25.
- How much more?
- If a chocolate bar is made of 8 rows and 6 columns, I would say 3 rows and 1 column.
- So?
- 3 rows is 18, 1 column is 8, so 8 x 6 = 25 + 18 + 8 = 51.
- Not entirely correct!
- That's true.
- So?
- I'll fix the method after dinner.

In 1492, the year the Arawaks discovered Columbus, a method called 'the ancient rule' was published in a book in Europe. It went like this.

- How much is 8 x 6?
- Make a 2 x 2 table and fill it in like this:

8 6
2 4

- Where did 2 and 4 come from?
- They are what is needed to make 8 and 6 reach 10.
- OK.
- Cross subtract: 8 - 4 = 4 and 6 - 2 = 4.
- What on earth!?
- Multiply the two lower numbers: 2 x 4 = 8.
- And?
- So 8 x 6 = 48. 4 from the cross subtraction and 8 from the bottom multiplication.
- Holy mackerel!
- One can never eat too much fish.

- I don't think this method always works!
- OK.
- Let me try 7 x 7.

7 7
3 3

- Cross subtraction gives 4 and 3 x 3 is 9, so the answer is 49. It worked!

- When you don't have paper available you can use your fingers for a similar method.
- Really?
- Let's try 8 x 6 again.
- OK.
- Hold your hands in front of you with the palms facing you.
- What for?
- Let the left middle finger touch the right little finger.
- Like this?



- Correct.
- And?
- Imagine a line just above the two touching fingers.
- OK.
- How many fingers do you have below the line?
- 3 on the left hand and 1 on the right.
- Add them up.
- 4.
- How many fingers do you have above the line?
- 2 on the left and 4 on the right.
- Multiply them.
- 8.
- There is your answer to 8 x 6.
- 4 and 8, 48. Neat!
- I agree.

- Does it always work?
- Why don't you find out?
- Let me try 7 x 7.
- OK.
- Which fingers should touch?
- Label your fingers from thumb to little finger with 10 to 6.
- So the ring fingers should touch?
- Right!
- I have 4 fingers below the line and 3 and 3 above, so 7 x 7 is 49 since 3 x 3 = 9.
- Great!

Ambition, Distraction, Uglification, and Derision

The Mock Turtle went on. “We had the best of educations . . . Reeling and Writhing, of course, to begin with, and then the different branches of Arithmetic—Ambition, Distraction, Uglification, and Derision.”

“I never heard of Uglification,” Alice ventured to say. “What is it?”

The Gryphon lifted up both its paws in surprise. “Never heard of uglifying!” it exclaimed. “You know what to beautify is, I suppose?”

“Yes,” said Alice, doubtfully: it means—to—make—anything—prettier.”

“Well, then,” the Gryphon went on, “if you don't know what to uglify is, you are a simpleton.”

If you want to learn more mathematics and logic from Lewis Carroll you could do worse than clicking here.

Mathematicians Stunned when Computer Reaches Final Digit of Pi

A team of Japanese researchers at a leading national university have upended the entire scientific world when it unexpectedly calculated the value of pi to 1.3511 trillion places, which is apparently the final digit in this number previously thought to be infinite.

"We don't understand," said visibly panicked project team member Makoto Kudo. "We were just trying to set a new world record for most digits calculated. We had no idea it would run out. Honestly!" - More

Talking math to your child

Does one have to be a mathematician to help someone with math? I believe the answer is no. To know some math is not a bad thing, but it is more important that you know how to talk to your child so he learns how to learn.

Seven ways to respond

I shall never forget my father’s answer when I asked him for help in translating some German words to Norwegian. “Use a dictionary, son!” What kind of help was that? I felt disgusted. He knew the answers and refused to help.

What I did not understand then, and what he might have explained, was that he wanted to put the onus on me. For one thing, because it was my homework, not his, but also because I should get used to use books for help. I have found there are seven ways to respond to a question for help.

1. Accepting the question, but offering no further response.
(“How do I find the volume of a cone?” – “That’s a very good question!”)

2. Encouraging the child to try more on his own.
(“Let’s see what you can find out. Try for another ten minutes.”)

3. Soliciting more information.
(“Please show me what you have tried.”)

4. General problem solving response.
(“Have you solved a similar problem before?”)

5. Specific problem solving response.
(“What do you know about volume of things?”)

6. Specific response
(“What is a cone? Can you draw one?”)

7. Very specific response
(“Study the example on page 54 in your textbook.”)

The aim is to help the child work his mind in such a way that the answer steps forward by itself. A grand order, therefore it is important not to expect miracles overnight.

Some other suggestions.

1. Listen a lot, talk a little. (The important person in the child, not you.)

2. Permit mistakes. (Without them learning can not take place.)

3. Enjoy yourself. (If you don’t value learning, neither will your child.)

4. Know problem solving. (Read “How to solve it” by George Polya. A classic from 1945.)

5. Ask stupid questions. (Ask anything that may help your child learn and have an enjoyable time.)

6. Listen, really listen. (Listen to meanings, not to words.)

You as a math teacher

I believe that to learn is to find answers to questions and to discover new questions. I believe you can help your child to do this even if you are not a math teacher.

The secret lies in the way you communicate with your child. You should aim to be a dialectician, someone who knows how to find truth through dialogue. Your child will not be a self-reliant thinker by accepting others ideas, he has to modify and enlarge his own. To give you a flavour of what I mean, here is a dialogue.

- How do I find 2/3 of 1 4/5? Should I divide or multiply?

- You should do neither. You should think.

- What do you mean?

- If you can't solve the problem, try to solve a simpler problem.

- Like what?

- What is 1/3 of 1 4/5?

- I have no idea!

- What is 1/3 of 21?

- One third of 21?

- That's right?

- That is 7.

- Why?

- Because 7 x 3 = 21.

- You mean, because 21 ÷ 3 = 7?

- That's the same thing.

- Then should not 1/3 of 1 4/5 be 1 4/5 ÷ 3?

- Yes, that makes sense.

- How much is 1 4/5 ÷ 3?

- 1 4/5 = 9/5, so the answer is 9/5 ÷ 3 = 9/5 ÷ 3/1 = 9/5 x 1/3 = 9/15.

- Very good! 1/3 of 1 4/5 equals 9/15. Now what about 2/3's?

- That must be more.

- How much more?

- Twice as much.

- So?

- 2 x 9/15 is 2/1 x 9/15 = 18/15.

- There you are! 2/3 of 1 4/5 equals 18/15.

- OK we found the answer. But, isn't there a faster way!?

- I like your attitude!

- So?

- You tell me! Look back at what we found!

- OK. First we divided by 3 then we multiplied by 2. I don't see a thing!

- 1 4/5 equals 9/5, right?

- Right.

- We found that 2/3 of 9/5 equals 18/15. Do you see any pattern?

- (After a while.) Oh yes! 2 x 9 = 18 and 3 x 5 = 15. So 2/3 of 9/5 = 2/3 x 9/5. All you have to do is to multiply!

- That's interesting. Do you think it always works?

- Come on! Of course it does! Why didn't you tell me right away?

- Because you did not want to know.

- But I did!

- You did not!

- I did.

- Did not.

- I did.

- Then I misunderstood you. I thought you meant "Teach me to think for myself. Teach me self reliance, endurance and self discipline. And most of all, teach me self confidence." That is what I thought you asked me.

- I am confused. I thought we were studying fractions, and not weird thinking and how to gain self confidence!

- To be confused is a good thing.

- Why?

- You don't want to know!

- I do.

- You do not.

- I do.

- It makes you think!

- I knew you were going to say that

One does not become a good dialectician overnight. I have been on it for more than twenty years and I am still learning. However, sometimes I do a good job. Some time ago, after having tried to help Sheena with a problem, she smiled at me and said: “Sir, I hate you!” “Why is that, Sheena?” “Because you make me think!”

School starts Tuesday

Be a Mathonaire

Would you like to try to become a Mathonaire? There are five levels to choose from and it is great fun. I didn't know the order of rotational symmetry of any rectangle, and it stopped me one step from the top on the easiest level. Play it here.

We haven't done division yet!

A firm has 10,000 bottles of lemonade to be delivered to supermarkets in crates, each of which has 36 bottles. How many carets should be ordered?

"In one class someone immediately said, "That's divisions" and someone else said, "We haven't done division yet!" I think that a couple of years previously this situation would have been met with consternation and no-one would have known what to do. Not now. Each class immediately set to work, in groups of their own choosing."

From an article by David Fielker called The Lemonade Bottles Problem. Read the entire article here.